Why do certain musical intervals sound pleasing to our ears? Are our musical preferences learned from our cultural heritage or are we born with a predisposition to find certain musical intervals consonant? Although the full answer to these questions is a complex and much studied issue you may be surprised that there is a compelling explanation as to why we find simple intervals such as a note and its fifth (e.g. notes C and G) pleasing. This explanation makes use of a number of the concepts that we studied so far this semester--how the ear works as a spectrum analyzer, the notion of critical bands, and the nature of complex tones. The level of detail given here is essentially a summary of the more extensive analysis that we will go over in class.

Pure Tones

From our earlier study of hearing we learned that when the ear is exposed to a pure tone a resonance is set up on the basilar membrane. The position of the resonance along the length of the basilar membrane depends on the frequency of the pure tone. Now when two pure tones are played at the same time there will be two resonances on the basilar membrane. If the pure tones are sufficiently close in frequency such that their critical bands overlap (you remember the concept of the critical band, don't you?) then the notes sound rough and unpleasant. If the notes are very close in frequency (less than 10 Hz difference) then beats can be heard and the sound is reasonably pleasant. Finally, if the two tones are identical (unison) the critical bands overlap exactly and the notes sound pleasing. From this simple description you might expect that pure tones would sound pleasing if the critical bands of the notes overlapped exactly OR if the frequencies are so far apart thet there is no critical band overlap. In tests of musically naive people this turns out to be exactly the case. On average such listeners find any two pure tones whose critical bands do not overlap to be pleasing (of course they find notes in unison pleasing as well). This sounds like it would make musical harmony easy--just play notes that are exactly the same or are well seperated in frequency! Ah! But musical notes are not pure tones. How does the situation change if we use the same criteria for complex tones? Read on.

Complex Tones

As we know well from class and the previous web pages (review!!), a complex tone consists of a harmonic series of frequencies. The pitch of the musical note created by this collection of frequencies is associated with the fundamental (lowest) frequency of the sequence. Now if we use the same consonance criteria as for pure tone we need to get two complex tones to have either perfect overlap or no overlap of the critical bands. You can instantly appreciate that the situation is more complex because we have many more frequencies and hence many more resonances along the basilar membrane. It becomes pretty difficult to get no overlap because even if the fundamental frequencies don't overlap there is bound to be some combination of the higher harmonics that has some critical band overlap leading to an unpleasant sound. It is easier to see how we arrive at pleasing (consonant) notes by looking at a couple of simple examples. First consider a musical note and the note one octave above it. Obviously these are universally considered consonant. Remember that the ear acts as a mechanical spectrum analyzerm, thus, let's examine the spectra of the base note and the octave as plotted in the figures below. The harmonics of the base note are plotted in blue in the top figure of the spectrum below whereas the harmonics of the octave note are plotted in red.

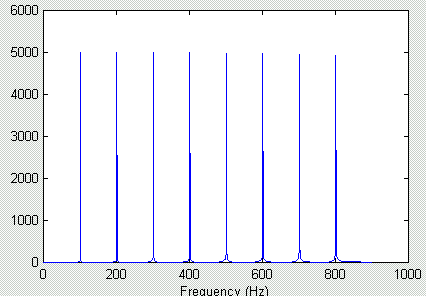
Spectrum of base note

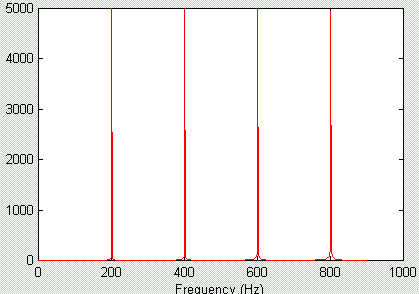
Spectrum of octave note

Examine the spectra. Clearly there is no overlap of the fundamental of the base note (at 100 Hz) and the second harmonic of the base note (200 Hz) lines up exactly with the fundamental of the octave. The 3rd harmonic of the base note (300 Hz) lies well away from any component in the octave whereas the 4th harmonic (400 Hz) lines up exactly with the second harmonic of the octave note. I could go on but you get the idea--these 2 consonant notes consist of frequeny components that are either well separated or exactly overlaping.

The interval of an octave is a very simple example of a consonant interval. Let's examine the ever so slightly more sophisticated interval of a fifth. You will remember that the interval of a fifth means that the ratio between the fundamental frequencies is 3/2. Thus, if we use the same frequency base note (fundamental = 100 Hz) the fundamental frequency of the note up a fifth is 150 Hz (= 100*3/2). Again I plot the spectra of the two notes below.

Spectrum of the base note

 

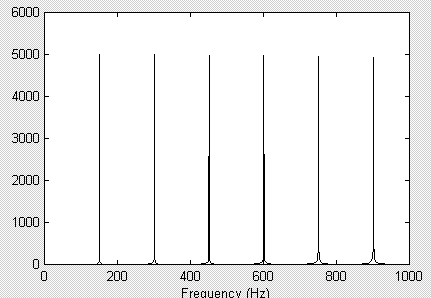
Spectrum of the fifth

Again notice that all of the harmonics in the two spectra either line up exactly OR are very far apart. For eample the fundamental of the fifth at 150 Hz lies exactly between the fundamental (100 Hz) and second harmonic (200 Hz) of the base note. The second harmonic of the fifth (300 Hz) aligns exactly with the 3rd harmonic of the base note. Again going to the higher harmonics it is easy to see that every other harmonic in the fifth aligns exactly with a harmonic in the base note. All other harmonics are located midway between the harmonics of the fifth.

Thus, to summarize, the simple notion is that consonance is associated with the absence of any critical band overlap. If there is critical band overlap (other than pretty much exact alignment) for any harmonics of two or more notes then there will be a "rough" and unpleasant sound -- the notes will be dissonant.

Deep Thoughts

Yes, Dr. Bill presents DEEP THOUGHTS. If this simple model of consonance is correct then musical intervals of fifth, fourth etc. should occur for people of all cultures! Why? Because it is based only on how the ear works as a spectrum analyzer, not on any cultural indoctrination. Is this true? I actually don't know, you musically inclined folks might try pursuing this as a special project topic. I did have a student in a past semester analyze the frequencies in a 9000 year old (and still playable!) bone flute which was discovered in China. His analysis showed that indeed the intervals of a fourth and fifth were present to high accuracy in this ancient instrument. Fascinating stuff, people.

Homework

Try the same exercise as I did for the octave and the fifth for the interval of a fourth. You do not need any program to plot things just assume a base note with a fundamental frequency of 100 Hz. Write out the frequencies of the first 10 harmonics of this base note. Then write out the harmonics of the note a fourth up from our base note. Which harmonics align?

Answer

Really too much to put down the full details here. As in class you should be able to show that every third harmonic aligns exactly between the 2 notes whereas the harmonics that do not align are spaced far apart in frequency so that there is none of that dreaded critical band overlap.

Special Project idea

I have never tried to duplicate the pure tone experiment that I describe above. It would not be too difficult to craft an experiment that tested whether
the consonance and dissonance of pure tones was associated with frequency separation. Also, it would be interesting to see if musically trained subjects showed a preference for intervals such as a fourth or fifth because they have been immersed in music to the degree that they recognize these intervals as musically special. Now if you could get such a test going as an online interactive type deal, that would be a project!