The ear converts the pressure amplitude variations of sound waves into sensations that we can perceive. The central point to be gleaned from this description is that the ear breaks up a sound into its component frequencies. This process of converting a signal in time (the incoming variations in the air pressure) into frequency is called spectral analysis.  Thus, in very basic terms the ear acts as a mechanical spectrum analyzer.

Consider the following schematic representation of the ear. (For a more realistic view of the anatomy of the ear click here). If you want WAY more detail about the ear and hearing go to this site and following the sound and hearing hyperlinks. 

 

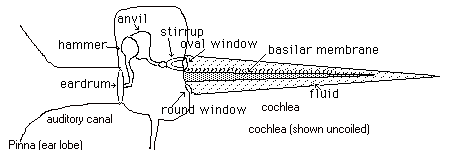
Here is a brief run down of the processes involved in hearing.

1. Sound waves enter the auditory canal and the pulsating pressure variations push on the eardrum.  Because the other side of the ear drum (known as the middle ear) is held at a fairly constant pressure the sound causes the eardrum to vibrate.

2. The vibrations of the ear drum are transferred to the three small bone sequence known as the hammer, anvil, and stirrup bones.  This mechanism is designed to effectively couple the sound vibrations from the air in thre outer ear into the fluid filled cochlea (inner ear). This task is accomplished in part by the lever action of the bones but more by the increase in pressure due to the fact that the stirrup bone pushes on a much smaller surface area than the surface area of the eardrum amplifying the pressure of the sound wave.

3. The fluid in the cochlea is vibrated with the frequencies of the incoming sound wave.  The basilar membrane is the element that separates these frequencies into components.  The Basilar membrane is a long structure that is stiff and hard near the round and oval windows and floppy and loose near its far end.  The membrane resonates at different positions along its length depending on what frequency is traveling in the cochlear fluid.  High frequencies are resonant near the hard stiff end whereas low frequencies are resonant near the far floppy end.  Nerves that run the length of the membrane detect the position of the resonance and hence the frequency (or frequencies) of the incoming sound. The typical length of the basilar membrane is about 35 mm.  There are 10 octaves of frequency resolution along the length of the membrane each octave occupies about 3.5 mm.  The figure below plots the frequency versus position along the membrane.

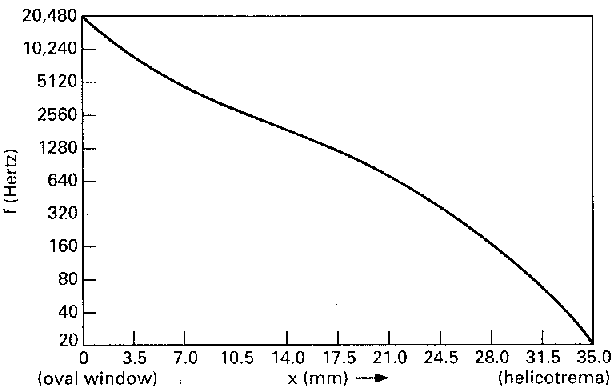
Note that the curve is approximately linear and that for every 3.5 mm travel along the horizontal axis (corresponding to distance along the length of the basilar membrane) the resonant frequency changes by a factor of 2. For example, in the first 3.5 mm the resonant frequency drops from 20,480 to 10,240 Hz.  Note also that the vertical scale is logarithmic; each equal sized increment up the frequency axis increases by a multiplicative factor of 2.

The ear acts as a mechanical spectrum analyzer splitting up sounds (oscillating pressure variations as a function of  time) into their component frequencies.  In other words the signal that is fed to our nerves and then is subsequently analyzed by our brains is proportional to the strength of each frequency in the sound.  As we will appreciate later this analysis in frequency rather than time is a very useful way to understand much more about a sound--particularly a musical sound--when it comes down to understanding concepts such as pitch, timbre, and the scientific basis of consonance.

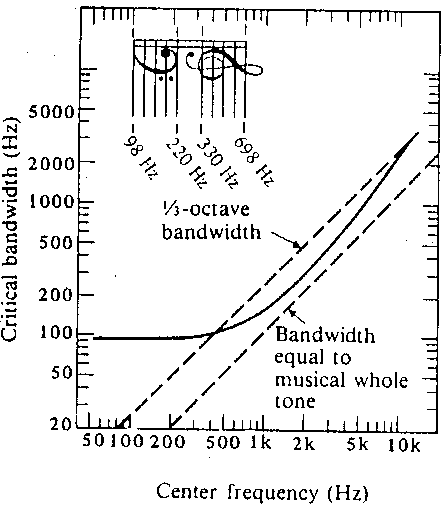
Unfortunately a mechanical spectrum analyzer is not perfect at homing in on just one single frequency exactly.  The resonance of the basilar membrane is not perfectly isolated to one particular position for a give pure tone input.  There is a width to the resonance.  Imagine listening to a pure tone of 640 Hz.  According to the figure above, the resonant position will be at 21 mm along the length of the basilar membrane.  However, that segment of the membrane cannot oscillate without making a small region either side of the 21 mm position oscillate also.  It's like grabbing the middle of your top lip and pulling it up and down.  The parts of your lip on either side get pulled up and down as well because the lip meat is all connected.  The net result is that a pure tone excites the nerves along the basilar membrane for a small length on either side of the resonance position.  Because the position along the membrane corresponds to frequency this statement is equivalent to saying that a pure tone excites nerves corresponding to a band of frequencies about the pure tone resonance.  This band of frequencies is called the critical band.   The critical band changes from the low to high frequencies.  The graph below shows the width of the critical band on the vertical axis versus the center frequency of the pure tone on the horizontal axis.  You should be able to read off the graph that at 100 Hz the critical band is about 90 Hz.  What is the critical band at 2000 Hz? (Answer: 200 Hz).

Even though the critical band is quite wide we are able to process the information given by the nerves in the basilar membrane to be able to discern very small differences between two pure tone frequencies.  The smallest interval between two frequencies that we can resolve with our ears is called the Just Noticeable Difference (JND) in frequency or frequency difference limen.  In the class demo we regularly have a couple of folks who can resolve frequencies at the 1 Hz difference level.  The rest of us mortals can typically resolve frequency differences of between 3 and 5 Hz.

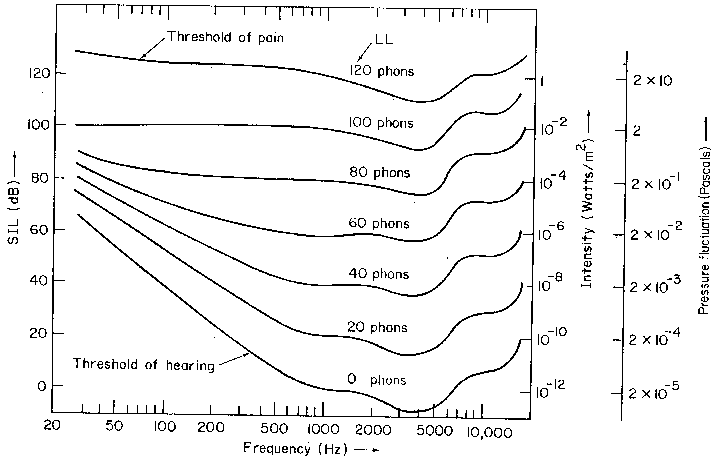
The final graph below is of the Fletcher-Munson curves of equal loudness.  For exams and quizzes it is important that you be able to interpret the graph.  It is easiest to consider the threshold of hearing line--the lowest curve on the figure.  The curve is 0 dB at 1000 Hz which is the standard reference level for the threshold of hearing.  At other frequencies this threshold of hearing deviates from 0 dB.  At low frequencies the threshold is much higher; for example, at 100 Hz a tone must be almost 40 dB before the average person can hear it.  In contrast at 4000 Hz sounds that are a few dB below 0 dB are audible.

The other curves are curves that represent equal loudness profiles. Note that for very loud sounds, 80 to 100 dB, the large difference in response between the low and mid frequencies disappears.

Note: What I hope that you know and understand from this section is the principle of operation of the ear as a frequency analyzer.  You should be able to understand and briefly explain terms such as critical band, masking, and frequency spectrum, and to be able to interpret and use the three graphs above.

Questions

1. Explain why masking by a pure tone occurs for a broader range of frequencies on the high side of the tone rather than on the low side of the tone.
2. What is the width of the critical band at 2 kHz and at 5 KHz?
3. At which end of the basilar membrane are high frequencies detected?
4. What is the approximate distribution of frequencies with distance along the basilar membrane? Explain why this distribution is logarithmic.
5. What is the frequency of the center (17.5 mm) portion of the basilar membrane?
6. Explain the function of the hammer, anvil, and stirrup bones.
7. Explain why it is important that the air in the middle ear is isolated from fast pressure changes.
8. What is the threshold of hearing in decibels at 200 Hz and at 4000 Hz?