We will have a number of class lectures on the basic concepts of Room and Auditorium acoustics. The purpose of this on-line segment is to teach you the process of calculating, albeit in an approximate way, the reverberation time of an enclosure. The web pages will give you some of the motivation and background; however, much of that material will be left for class discussion.

The process is fairly straightforward. In this page I will give you a brief overview of reverberant sound. In the next I will define the quantities reverberation time and absorption coefficient and show you how to calculate the absorbtion of a room. Finally in the third page I will show how these quantities are combined to give an approximate method of calculating the reverberation time of an enclosure.

In much of our dealing with sound waves thus far we have often assumed the so-called free-field approximation. The free-field model assumes that sound waves are emitted from a point source and travel outward as spherical waves never coming into contact with any reflecting surfaces. Although this model is a convenient simplification in many situations it does not take a great deal of thought to realize that free-field conditions are almost impossible to realize in practice. On the contrary, many, if not most, acoustics systems of interest involve sound sources and listeners that are located inside an enclosure--for example a classroom or an auditorium. What changes from the free-field conditions result from enclosing the source and sound receiver? Consider the two dudes in the figure below:

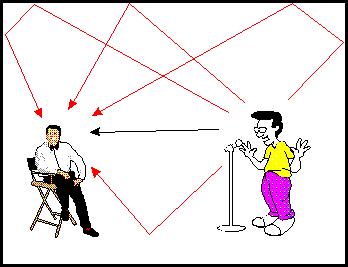
One is the source of sound, the other the receiver--it's pretty obvious which is which. The black line represents the so-calleddirect soundthat the receiver hears straight from the source. This sound is the onlys ound that would be heard in free field. However, in an enclosure in addition to the direct sound the hearer also receives the sound reflected off the walls of the room--the reverberant sound. The first of these reflections are represented by the red lines.

Because the walls are not perfectly reflecting--some energy is absorbed with each reflection--the reverberant sound eventually decays away after a sufficient number of reflections.

The acoustic properties of the materials that make up the reflecting surfaces in the room will thus play a part in determining the duration of the reverberation. We will see how to quantify these properties in the next section.

Definition of Reverberation Time

As you may have noticed with our technical study of acoustics thus far, scientists like to quantify properties by assigning them some numerical value. In this case we want to quantify the reverberation time--the time that it takes for a signal in an enclosure to decay after the sound source is turned off. To understand the definition of reverberation time it is useful to consider the following simplified scenario: imagine that our sound source in the above enclosure (Mr. Pink Pants) emits a constant sound for a few seconds, what is the sound perceived by our listener and how does it differ in the enclosure compared to free field? The first sound to reach the listener will be the direct sound. In the graph below the direct sound is represented by the dark rectangle. The next sound to reach the listener will be the various first reflections from the walls of the enclosure. These sounds are represented by the red rectangles. The path length differences for all the different paths that the reflected sound can follow to get from the source to the listener mean that the sound builds up gradually as a function of time.

 

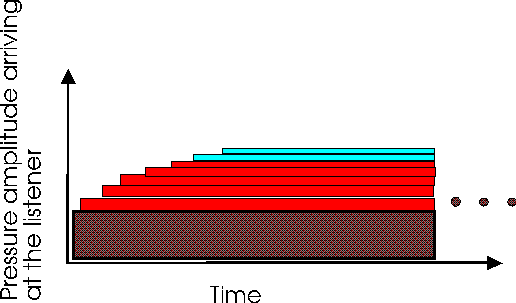
The light blue rectangles represent sound that has suffered multiple reflections around the room, perhaps passing by the listener many times. The figure is not the greatest but you can get the idea. Note that the final steady state sound level in an enclosure is higher than the sound level in free field; remember the dark bottom rectangle is the direct sound that would be heard in free field. In reality the rise of the sound up to steady state would not really be step-like as in the figure, rather, because of the many different reflection paths, it would be smooth as in the (much better looking) graph below.

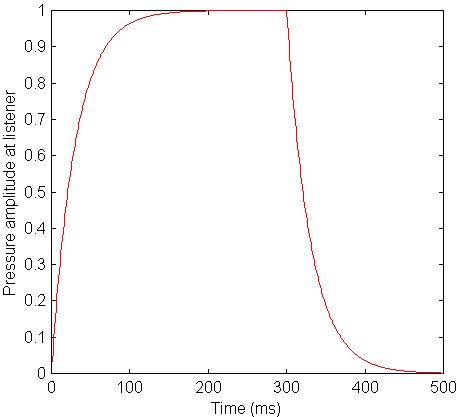
This figure shows not only the exponential rise as the sound builds up to its steady state value but also the decay after the sound is turned off. The build up and decay times are identical because the processes are pretty much the same. When the sound is turned off the direct sound disappears first (the shortest path to the listener), then the fairly strong first reflection signals disappear, then the ever weaker multiple reflections.

It is the decay curve at the turning off of the sound source that is used to make a quantative definition of reverberation time.

The agreed upon standard for the reverberation time is the time it takes for the signal to drop by 60 dB from its steady state value after the sound is turned off.

Questions to ponder (no answers yet we'll discuss these points in class).

1. A drop of 60 dB corresponds to how big a change in pressure amplitude? intensity?
2. What does the steady state condition imply about the amount of energy being absorbed by the walls of the enclosure?
3. If you wanted to emulate free-field conditions in an enclosure what property would the walls have to have?

Forward ->