Motion that repeats in a regular pattern over and over again is called periodic motion.  As we will come to appreciate, periodic motion is crucial to the production of musical tones.  However, to begin our analysis we look at the most basic type of periodic motion called simple harmonic motion. Simple harmonic motion occurs in a myriad of different forms in the everyday world; for example, a person bouncing on the end of a diving board, a child in a swing, or your cousin's funky car (you know the one with no shocks) that bounces down the road like a low-rider every time you hit a bump.

Physicists like simple harmonic motion (let's begin abbreviating it SHM) because every example of SHM is based on the same underlying physical principle and all examples of SHM have the same, very straightforward, mathematical description.

What is the physical principle?  SHM occurs around an equilibrium position when a mass is subject to a linear restoring force.  A linear restoring force is one that gets progressively larger with diplacement from the equilibrium position.  The best example of this is a spring.  The more you stretch a spring the larger the force trying to get the spring back to its original shape.

What is the simple mathematical form of SHM motion?  The displacement of the oscillating mass varies sinusoidally (whoa, big word!) as a function of time.  [sinusoidal means like a sine function.  You remember sine and cosine functions from your trig classes don't you?].  We won't do too much with the formula but here it is:

y = A sin(2pf t)

What you do need to know is the meaning of the symbols in the formula and be able to identify these parameters in different examples of SHM.  Below is a animated image that shows how the displacement of a simple harmonic oscillator varies with time.  Warning! I made the image myself and I am no Walt Disney animator.  It is supposed to represent a mass on a rubber band or spring and the graph on the right plots the position, y, as a function of time, t,  along the x-axis.

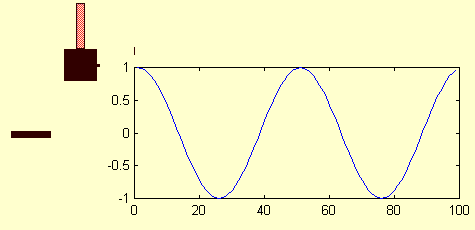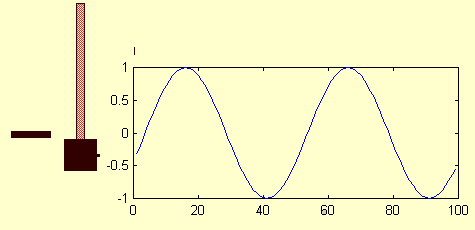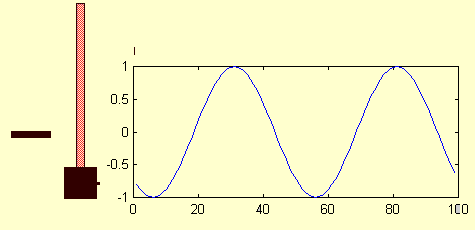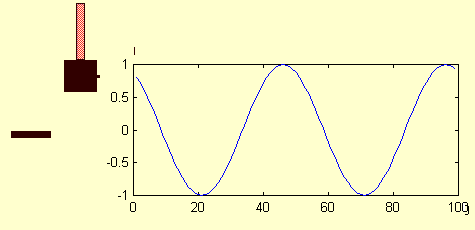
Here are the definitions of the parameters relevant to SHM:

Amplitude, A.

The amplitude of the oscillation is the maximum distance that the oscillating object moves away from the equilibrium position.  That last phrase is very important.  Many people make the mistake of taking the peak-to-peak amplitude of the sinusoidal oscillation.  Nope! it is only the distance from the center to one extreme.  So in the figure above the amplitude of the oscillation is 1 (that is the distance from the equilibrium position at 0 out to the extreme of the motion at 1 on the graph).

Frequency, f

The frequency of the oscillation is the number of oscillations per second.  Remember an oscillation is one complete cycle of the oscillator.

Period, T.

The period is the time for the oscillator to complete one cycle.  It should not be a big stretch to figure out that the frequency and period are related (actually they are just different ways of expressing the same information).

f = 1/T

The key feature of SHM is that the period or frequency of the motion does not depend on the amplitude of the oscillation.  In other words whether I set a mass on a spring oscillating with a large amplitude oscillation or a small amplitude oscillation the period of the SHM remains the same and it depends only on the physical structure of the oscillator.  From a practical viewpoint this effect was used to make the first accurate clocks.  A pendulum takes the same time to make one oscillation even though the amplitude of the oscillations dies down with time. The period does not change.

Resonance

Resonance is another vital concept in acoustics.  We will discuss resonance in much more detail in class but here is a simple description for an everyday simple harmonic oscillator system--a child in a swing.  For any given length of the chain of the swing there is a corresponding natural period of oscillation.  (Surprisingly, the period of oscillation does not depend on the mass of the person sitting in the swing.)  When we push a person in a swing we instinctively give them energy exactly at the natural frequency of oscillation because we only give a push when the swing is just past its maximum amplitude and moving away from us. Even though we are only giving the swing small pushes, the amplitude of oscillation of the swing grows rapidly.  We are said to be driving the oscillator at its resonant frequency.  If we instead chose to push the swing at a much higher frequency we would be pushing at a variety of different points in the swing cycle.  At some of those times the swing would be moving towards us while we are pushing away thus we would be counteracting the growth in amplitude of the swing.  The net result is that the same number of equal sized small pushes would just make the swing move erratically in a small region around the equilibrium position.  This jerky erratic motion can, of course, really tick off the swingee!  The net result is that if we input even a small amount of energy into a SHM oscillator at its natural frequency of oscillation the result is large amplitude oscillations.

Damping

Damping is the term used to describe the loss of energy with each cycle of a simple harmonic oscillator.  The simple harmonic oscillator begins with a certain amount of energy, for example when we compress or stretch the spring attached to a mass.  In an ideal simple harmonic oscillator this energy would remain the same forever.  Note that the energy converts between kinetic energy (energy associated with a moving mass) and potential energy (energy stored in a non-moving form such as that stored in a stretched or compressed spring). In the real world, the mechanical energy of the simple harmonic oscillator is always lost to heat due to air resistance or friction in a bearing or in a spring. For a lightly damped simple harmonic oscillator the fraction of energy lost each cycle is small and shows up as a slight reduction in the amplitude on each successive oscillation. However, as we said above the period does not change even in this lightly damped case.

Problems

1. A pendulum makes 30 complete oscillations in 20 seconds—what is the period of 1 oscillation?  What is the frequency of the pendulum?  What are the units of frequency?

2. A point along a vibrating guitar string oscillates in simple harmonic fashion.  If instead the period of a vibrating string increased as the amplitude of the vibration died down, what would be the musical consequence?  Specifically, would the pitch of the note rise, fall, or stay the same as the sound decayed away?

3. A simple harmonic oscillator has a natural frequency of 440 Hz.  If forces with the following periods drive the oscillator, which would produce the largest amplitude of oscillation?

   (a)  0.005 s    (b) 0.00227 s      (c) 0.00144 s

4. The frequency range of human hearing is from 50 Hz to about 20 kHz.  What is the period of oscillations at these two frequency extremes?  What are the units of period?  What are the units of frequency?

5. Estimate the frequency of the simple harmonic oscillator in my not-very-professional animation above. Use your watch to time it. Ignore the numbers on the axis along the bottom.

6. The natural frequency of a Helmholtz resonator (like the wine bottle we examined in class) is given by the equation
   f = ^v/_2π √ ^a/ Vl

   
   where v=344 ms-1 is the speed of sound, a is the area of the opening, l is the length of the neck, and V is the volume of the air enclosed.

   1. For a certain acoustic guitar body the enclosed volume of air is 0.04 m3, the area of the opening is 2.5 x 10-3 m2, and the length of the neck is 5 x 10-3 m. What is the natural frequency of this Helmholtz resonator?

   2. You want to increase the frequency of the Helmholtz resonance for the guitar.  How might you best accomplish this task?

   3. Installed electronics inside the guitar body reduce the volume of air enclosed from the original 0.04 m3.  Does this volume reduction result in an increase or decrease in the Helmholtz resonance frequency?

7. What length would you need to make a pendulum to have a period of 1 s?  Remember
   

   T = 2π √ ^l/ g

   where g=9.8 ms-2.

8. Define in words the terms resonance, damping, period, and frequency.

9. For a lightly damped simple harmonic oscillator which of the following quantities change over time

   1. period (b) frequency (c) amplitude (d) stored energy.

10. Explain in words what is meant by a linear restoring force.

11. The period of a mass on a spring is given by the equation
    

    T = 2π √ ^M/ _K

    A spring has a spring constant K=100 N/m.  When an unknown mass, M, is attached to the spring the mass srping system will oscillate with a frequency of 5 Hz.  What is the value of the unknown mass?