I like to start the discussion of standing waves with the demonstration of a sine wave oscillator attached to a string which is held fixed at the other end. The experiment gives the following results. As I adjust the frequency of the oscillator from the lowest value of up in frequency, I can see that the string is bouncing around but there is no very large definable pattern until I hit one particular frequency at which the string has a very large amplitude pattern that looks like the following figure.

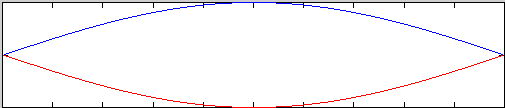
The blue and red lines show the extremes of the motion of the string--the string keeps oscillating back and forth with a large amplitude between these extremes. If I adjust the frequency a little higher, the string returns to its random small amplitude motion. If I keep increasing the frequency I will get to a point when the string again displays a large amplitude oscillation but with the following pattern.

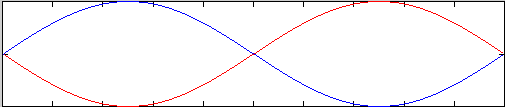
Again increasing frequency I can get the following patterns at successively higher frequencies.

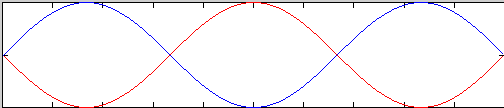
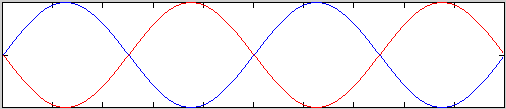
I could go on to even higher frequencies and get the higher order patterns in the sequence. When I do the demo in class I write down the frequencies at which each of these "resonances" occurs and I find that they have they are related. The frequency of any particular pattern is an integer (a whole number like 1,2,3,4..) multiplied by the frequency of the first resonance shown in the top figure. In other words if the lowest frequency is 5 Hz then the next resonance occurs at 2 x 5 Hz = 10 Hz, the next at 15 Hz, then at 20 Hz etc.

We have described the phenomenon now let's see if we can understand and describe mathematically what's going on. I have already used the word resonance to describe the effect and that model is an important starting point in coming up with a mental picture of what is happening. We first described the concept of resonance with reference to the simple harmonic oscillator (SHO). The SHO has only one natural frequency of oscillation. If we push on the oscillator (drive the oscillator) at its natural frequency we get a big amplitude oscillation. I used the example of pushing a child in a swing as an example of how we naturally push at the resonant frequency by waiting until the child makes a full swing (one oscillation) before putting in the next push. The same model is a good way to start understanding the problem of waves on a string. We launch a wave and it travels down the string, it's reflected from the tied down end, the reflected wave (inverted because it hit a solid boundary) returns to the starting point and is reflected again. If we launch another wave just as the first has made its return to the oscillator we will be pumping energy into the wave just as we did with the child in the swing.

I can apply some mathematics to figure out what frequency I will need to set my oscillator at to fulfill the condition I just described. If the wave travels at a velocity v, and the length of the string is L, then I know that the time (T) for the wave to make the trip to the end of the string and back is T = 2L/v. If I launch a wave every T seconds I will get that first resonance I described in the first figure above. In terms of frequency rather than time I need to set my oscillator to f = 1/T = v/2L.

Now that we understand the first resonance how do we explain the others? It's pretty easy. If I decide not to wait the full time for the wave to come back but rather I launch a second wave at exactly the time the first wave reaches the end of the string I now have two launched waves on the string at the same time. Obviously, I have to put the waves out with only half the period T from before or in other words with twice the frequency. The frequency of the second resonance is thus f2 = 2v/2L. I could keep going with this argument to launching more and more waves to get the higher resonance's. The net result is that the general formula for the n'th resonance (n is an integer) is

fn = nv/2L

Mode Picture

The foregoing description is in terms of the time it takes for the pulse to make the round trip. You can get the same formula from the mode or standing wave picture of the resonances. In this method you just draw a diagram as I did above that shows the standing wave at its extremes. By looking at one extreme or the other (either the red or the blue curve) you can relate the wavelength to the length of the string. If you know the wavelength of the wave you know its frequency from the fundamental wave formula v=fl. Let's look at the first picture above. From the blue part of the curve we can see that in a length L--the length of the string--only a half a wave has been completed. Thus, the wavelength of this lowest frequency wave is f = v/l = v/2L. In the second picture the blue curve completes exactly one full wave in the length L and thus f = v/l = v/L = 2v/2L. Again I could keep going and the end result would be the same relation above that we obtained from the time picture.

In practice the mode picture is a quick way of figuring out the frequencies of the harmonics in other more complicated situations. In the problems listed below I ask you to find the frequencies for various situations. Be sure to try these problems to make sure you actually understand how to use this mode picture in practice.

Air in Tubes

Strings are fairly straightforward to work with in the mode picture because we know that the two ends of the string are tied down and must be nodes. With that constraint it is relatively easy to draw the standing wave modes beginning with the lowest frequency (longest wavelength). With air in tubes the situation is a bit more complicated because the boundary condition is not quite as easy to understand. In class I describe the fact that we can look at a standing sound wave in a tube in either pressure amplitude or in a new quantity called displacement. Pressure amplitude is the variation of the pressure above or below atmospheric pressure down the length of a tube. Displacement is a measure of how far the molecules of the air had to move to create this pressure variation. In the figure below the blue curve represents a plot of pressure amplitude.

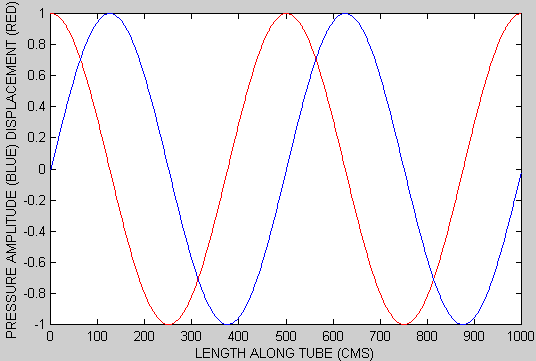
To create a high pressure region the air molecules from both directions along the tube must scrunch in (pack closer). Thus, at a pressure maximum the displacement--how far along the tube the molecules at that point have moved away from their equilibrium positions--is zero. Similarly, at a pressure minimum the molecules on both sides have moved away to create a lower pressure region and the displacement is again zero. Between the maximum and minimum the displacement varies sinusoidally to create the sinusoidal pressure variation. The net result is that the pressure amplitude and displacement curves are 90 degrees out of phase. The displacement is plotted as the red curve in the figure above. A 90 degree phase difference means that a pressure amplitude node corresponds to a displacement antinode and vice versa.

Whay have we introduced the concept of displacement? Well when we want to examine the boundary condition at the closed end of a tube this concept is very useful. At a closed end the displacement must be zero as the atoms cannot move into the solid wall at the end of the tube. In contrast at the open end of a tube the pressure amplitude must be a node. Imagine if it was not a node rather it was held at some minimum (or maximum) pressure. If this were the case, at the open end the atmosphere would rush in to cancel the minimum pressure. A node of pressure amplitude is the only stable alternative.

With these criteria in mind we can draw the standing wave modes in an air-filled tube. Let's do the tube closed at one end since it has a different boundary condition at each end. At the closed end we must have a displacement node. At the open end we must have a pressure node. Because we cannot draw a mode picture that mixes pressure amplitude and displacement let's choose to draw the condition in terms of displacement only. Thus, at the open end a pressure amplitude node is equivalent to a displacement antinode. What is the longest wavelength that satisfies both these conditions? It's drawn in the figure below.

How much of a wavelength does this represent? It is only 1/4 of a full wavelength thus the wavelength corresponding to this mode is l = 4L. The frequency is f = v/4L, where v is the speed of sound in air.

Drawing the higher modes takes a bit of thought on your part. Here is the next highest mode--remember the condition that it has to satisfy is that there be a node at the left end and an antinode ath the right end.

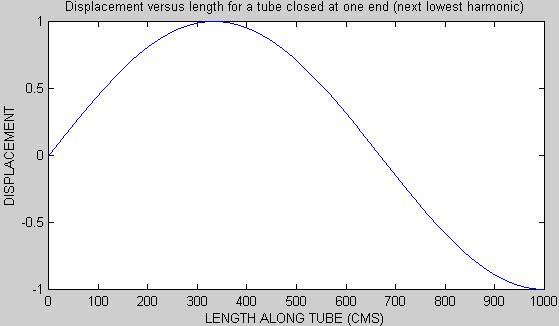
The tube of length L contains 3/4 of a full wavelength thus the wavelength is 4L/3. Make sure you know how I got this! As I said it takes some thought on your part. With the wavelength the frequency is just f = 3v/4L. Note that this is a factor of 3 times the fundamental frequency. For a tube closed at one end there are no even harmonics. You will appreciate this more fully by doing question 3 below.

That's it. Try the questions and ask if you get hung up!

Questions

1. Draw the first 4 allowed standing waves on a string of length L. From your drawing what is the wavelength of the fourth harmonic? How many nodes and antinodes are there for the fourth harmonic standing wave?

2. For the string in question 4 you find that the fundamental frequency is 250 Hz. If the string is 2 m long what is the wave speed on the string? What is the frequency of the fourth harmonic?

3. Draw the first 4 allowed standing waves in a tube of length L closed at one end. What is the constraint on the displacement and pressure at the open and closed ends of the tube that guides you in drawing the standing waves? Be clear as to what you are plotting (displacement or pressure) when you draw the representations of the standing waves. For each of the first 4 standing waves write down the associated wavelength. Use the wave relation v = f l to write the frequency of each harmonic in terms of the speed of sound v and the length of the tube L.

4. Using your information from question 3, design a didjeridu that has a fundamental note of 110 Hz?

5. Here is a real question to me from James Gordon--a biologist from the University of Leeds (UK) who is trying to use didjeridus as an elephant deterrent. Design a didjeridu whose fundamental (lowest frequency) is the same as the third harmonic of a didjeridu of length 5.66m.

6. Calculate the fundamental and next higher harmonic frequencies for the tube considered in question 3 given that the tube is 0.6 m long and the speed of sound in air is 344 m/s.

7. On the Planet Zeppo the atmosphere consists largely of Helium and the speed of sound is 688 m/s, about twice the speed of sound on earth. Will the fundamental frequency of a trumpet be higher or lower when played on Zeppo? If you've ever watched those Jacques Cousteau deep-sea diving shows you will know the answer.