The study of waves is clearly an important subject in acoustics because sound energy is transmitted by waves traveling though air. Furthermore, it turns out that the properties of waves on strings and in hollow tubes (one-dimensional systems) results in a particular harmonic structure that leads to musical tones.

To begin we define what a wave is:

A wave is a propagating disturbance in a medium that transmits energy without any net movement of mass.

In other words the energy in the wave moves from point A to point B without moving any material from A to B.   After transmission of wave energy the medium is left pretty much the way it was before the wave traveled through. Contrast this wave picture of energy transfer to that of being beaned by someone throwing a baseball: energy is transmitted but so is the mass of the baseball--not a wave-like process becasue mass is transferred.

A simple example of wave excitation occurs when a medium (such as a string) is held in contact with a simple harmonic oscillator. As the oscillator bobs up and down waves are launched on the string. If the oscillator has a frequency f we know that it bobs up and down f times in one second.  Each time it makes a complete oscillation it launches one wave onto the string.  If the distance along the string for one wavelength is  l metersthen the speed of the waves v (that is the speed you travel if you surf along the crest of one of the launched waves) is given by

v = f l

This formula is a fundamental one that describes waves of all types, not only sound.  In the case of sound waves in air the velocity v = 344 ms-1 (approximately).   Because the speed is a constant for all frequencies it is easy to convert between wavelength and frequency using the formula above.

The figure below shows the sine wave shape of a wave launched by attaching a stretched string to a simple harmonic oscillator.  Note how the amplitude of the wave is defined as being from the center equilibrium position of the string to the maximum.  Note also the definition of a wavelength l.

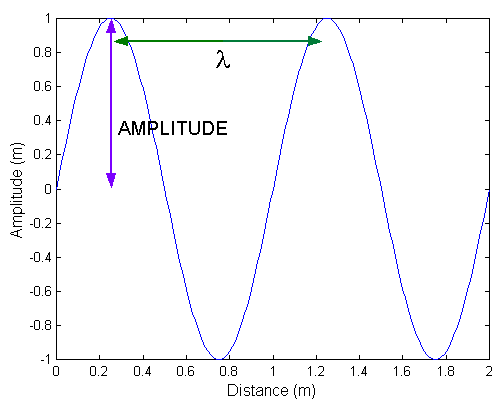
Remember that this picture is meant to be a side-on snapshot of the string at a fixed instant in time.  At the next instant the entire sine pattern will have moved as the wave travels.  Actually if you look at my cheesy animation in the simple harmonic oscillator page you get a pretty good idea of what the wave patterns looks like as the sine wave travels to the right away from the oscillator.

Three Important Wave Properties

There are three wave properties that are universal (that is they apply to all wave excitations) and that will be important to the systems we will be analyzing in the next few weeks.

1. Reflection.

When a wave hits the boundary between two media some of the wave energy is transmitted and some is reflected.  For waves in two- and three-dimensions the angle that the wave is reflected is equal to the angle of incidence--just like a ball hitting the side cushion of a pool table.  This property is very important for optics but its effect is less easy to appreciate for acoustic waves.
The other reflection property of waves that will be very important is that there is a phase change of a wave reflected from a "hard" boundary.   The computer simulations that I showed in class are probably the best way to get this concept lodged in your head (What? You missed class! Bad dog, no biscuit.)  A physical example of a hard boundaries are the ends of a guitar string which are tightly held at the nut and bridge. A phase change on reflection means that an upward going pulse that is incident on the end of the string is reflected as a downward going pulse.  In contrast, at a soft boundary, such as the free end of a harmonica reed, the reflected wave is not inverted.

2. Diffraction.

When a wave passes through a small opening it spreads out, this process is called diffraction.  This process allows us to hear around corners because the sound is diffracted through an open door or window and fills the room.  Again the simulation in class should have given you an intuitive physical picture of what is happening.  The big question is what constitutes a "small" opening.  Small in this case means if the opening is about the same size (or smaller) that the wavelength of the sound.  From our equation above you will become good at figuring out the wavelength for given sound frequencies.

3. Superposition.

The last important property of waves is a concept called superposition.  There are actually two aspects. First, two (or more) waves can pass through the same physical space and their propagation properties (like direction, speed, etc) are not affected by the presence of the other waves.  Waves do not collide with each other and they do not bounce and ricochet like physical objects.  My optical example is that the spot of a laser pointer on the wall is the same whether the lights in the room are on or off!

The second aspect is that at a point in space at which the waves cross each other the ampltitude is just the sum of the amplitudes that the two individual waves would have created at that point.  Remember amplitudes can be positive or negative so waves can sometime cancel each other out at one point in space.

Beats

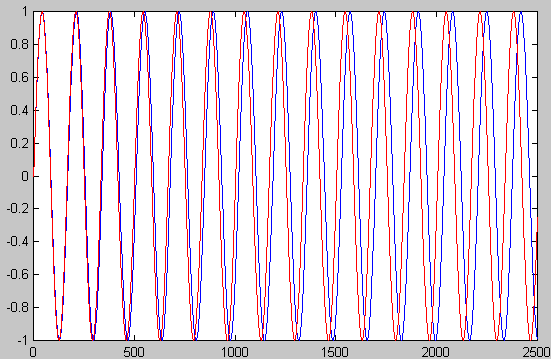
Beating of two sine waves is an example of wave superposition.  The wave amplitude at a point in space is just the sum of the wave amplitudes arriving at that point.  Look at the figure below: the red and blue curves represent pure sine waves with slightly different wavelengths (and of course slightly different frequencies).  Note that although they start together on the right hand side, by the left of the plot they are getting out of phase.

 

If you were listening to this note you would hear the superposition, that is you would just add the two amplitudes at each point.  The result would be something like this figure.

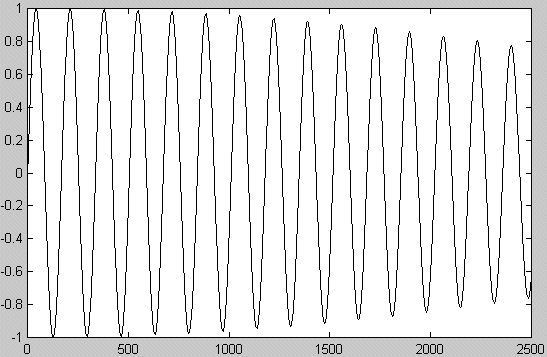
If I went for a much longer plot of the two waves there would come a point at which the sum of the two waves would be almost zero and then it would grow again as the two waves got back into phase.
It is the slow change between in-phase and out-of-phase that we hear as the beat.

The beat frequency is just the difference between the actual frequencies of the two notes.

fbeat = |f1 -f2|

Waves in Three Dimensions

In this class we will be examining waves in one-dimension, such as on strings or in tubes; two dimensions, such as on plates or drum heads; and three dimensions, such as sound in a room or in the open air.  Here I want to emphasize one point about the drop-off in energy of waves in three dimensions.  Consider a perfect three-dimensional wave launched from a small source and radiating sound in all directions. The sound waves move away from the source and the crests of the waves form a series of concentric spheres centered on the sound source. Of course each crest is separated from the next by a distance of l, the wavelength, as measured along a line radially outward from the source. This model of sound in three dimensions is called free field sound.  It is an idealized case that is easy to study but actually kind of hard to implement in practice (Why? you should be able to figure out why.)

Now as the wave expands the energy is spread out over a larger surface area.  Thus the intensity of the wave, defined as the energy per second passing through a given area, decreases as we move away from a source.  A sound gets harder to hear as we move away from it.  The mathematical expression for the drop-off is

I = W/4pR2

where W is the power of the source (measured in Watts = Joules/second) and R is the distance from the source in meters.  You should hopefully recognize that 4pR2 is the area of a sphere!

The inverse squared drop off in sound intensity in free field will be important when we come to consider  how the decibel level of sound drops off with distance.  Another basic result of the above formula is that if you double your distance from a source the sound intensity (in free field) drops by a factor of 4, if you triple your distance the intensity drops off by 9, etc.

The Doppler Effect

In class I derived the expression for the Doppler effect when the source is moving.  The important concept to get is that the waves, once they are emitted, move through the medium at the speed of sound regardless of the speed of the source.  If the source is moving towards you then the wavefronts are scrunched together leading to an increase in the rate at which the wavefronts hit your ear.  This process results in an increase in frequency compared to a stationary source.  Look at this online demo to see the wavefront picture.  The final result is that the Doppler shifted frequency f' is related to the frequency f by

f' = fv/(v-V)

where v is the speed of sound and V is the speed of the source.

Problems (a few more and the answers will be added later)

1. You are riding at the front of a moving train.  There is a siren sounding a constant tone at the other end of the train. Do you hear this tone Doppler shifted in frequency? Why or why not?

2. You are sitting in a child’s swing oscillating back and forth (in simple harmonic motion!).  In front of you on the ground there is a speaker giving out a constant tone.  For which parts of the swing cycle will the tone be shifted up in frequency?  For which parts will it be shifted down? Are there points in the cycle where you hear the unshifted tone?  If so, at which points in the swing cycle are these points?

3. The frequency range of human hearing is from about 50 Hz to about 20kHz.  If the speed of sound in air is 344 m/s find the wavelength of the highest and lowest audible frequencies.  Find the wavelength of the note A4 = 440 Hz.

4. Elephants can hear the frequency range 16 Hz-12 kHz (they buy a lot of Barry White CD’s).  What wavelength range does this correspond to?  Bats, who use sound for navigation, can hear from 1 kHz-150 kHz.  They obviously have little time for human music because the lowest human “note” they can hear is C6 (two octaves above middle C).  What wavelength does 150 kHz correspond to?  Why might this high frequency (short wavelength) be important for navigation?

5. A piston vibrating in simple harmonic motion launches waves on a stretched string.  You measure the speed of the waves to be 690 m/s and the wavelength of the waves to be 3.45 meters.  What is the period (in seconds) of the simple harmonic oscillator that launches the waves?

6. You pluck a string which is tied down at both ends and launch a pulse that travels the length of the string, is reflected at the tied end, travels back to the other end, is reflected and returns to your original launching point.   If the string is 1.5 m long and the wave speed on the string is 1200 m/s how long does the wave take to make the round trip?   If the pulse keeps on traveling around and around on the string what is the frequency with which it returns to the starting point?  When the pulse returns to the starting point after one round trip is it inverted or the same way up as when it started?

7. Diffraction occurs when the wavelength of the wave is about the same size or larger than the opening through which it is passing.   Diffraction becomes negligible when the wavelength is much smaller than the opening through which it is passing.  If we assume that there is little diffraction when the wavelength is 20 times smaller than the opening find the frequency above which diffraction through a square opening 1m x1m can be neglected.  Take the speed of sound to be 344 m/s.

8. At what sound frequency does the wavelength of sound equal the diameter of the following.

   1. a 15 inch woofer [ 0.38 meters in diameter]

   2. a 3 inch tweeter [0.076 meters in diameter]

       Remember, diffraction will only be strong for wavelengths that are about the same size as the opening or larger thus these frequencies tell you the transition between the speaker filling the room with sound versus being directional.

9. An ultrasonic tape measure works by sending out a short sound pulse at a frequency above 20 kHz (the ultrasonic regime).  Distance to an object is determined by the time it takes for the echo to return.  How much time will it take for the echo to return from a wall 5m away?  Take the speed of sound to be 344 m/s.

10. Two tones sounded together have a beat frequency of 5 Hz.  One of the tones has a frequency of 261 Hz.  What are the possible values for the frequency of the second tone?

11. In problem 9 the known tone is altered from 261 Hz to 263 Hz.  The beat frequency now becomes 3 Hz.  What is the frequency of the unknown tone?

12. A small speaker suspended in the middle of a large room gives out a constant intensity sound wave. Assume that the wave given out is a spherical wave.  At a distance of 1 m from the speaker my ear intercepts 1 microwatt of power.  How much power does my ear intercept at 2m?  At 3m?  At 10m?

13. The area of an eardrum is about 0.55 cm2.  Normal conversation creates sound pressure variations at the eardrum of about 10-2 N/m2.  What approximate force is exerted on the eardrum during normal conversation?  [Remember Force = Pressure x Area].