MATH 1710 - K Transitional College Algebra

Refresher vocabulary (vocabulary from MATH 1000)

R.1

Pythagorean Theorem stated in words: The sum of the squares of the lengths of the legs of a right triangle is equal to the square of the length of the hypotenuse.

. . . stated in symbols: a² + b² = c²

where a and b symbolize the lengths of the legs and c symbolizes the length of the hypotenuse.

To begin to learn the theorem stated above, some definitions need to be known, for example:

sum (noun form)
squares (noun and verb forms)
legs (noun form)
right triangle (noun form)
equal (verb form)
hypotenuse (noun form)

What additional terminology do you need to know? Look for anything in the two statements that you are uncertain about and add to this list.

R.2 Integer Exponents

To understand the title of this section you need to understand what an integer is, what an exponent is, and how exponents work.

An integer is a symbol for a particular type of number that is a member of the set of Integers. The Integers (short way to refer to the entire set, or group) can be described as the set of numbers that include zero and every other number that can be generated by increasing or decreasing by ones.

Set: a collection of numbers or elements that have common characteristics.

Questions: Are fractions in the Integers? Are all Integers negative? Are any Integers negative? Is zero an Integer

Symbolically: . . . -3, -2, -1, 0, 1, 2, 3, . . .

An exponent is the part of an exponential expression counts the number of times that the base is used as a factor in the product. The exponent is written as a superscript number immediately to the right of the base.

An exponential expression is a way to represent a single value that is calculated by raising the base to a power shown by an exponent.

Base: the number that is used as a factor in an exponential expression (hang on, IÕll draw a picture that will help explain it).

Power: the exponent read as an ordinal number (first, second, third, so on).

Superscript: any symbol written above the line, such as a footnote symbol or exponent.

Here is the picture I promised:

 

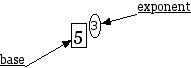
How exponents work: the exponential expression tells us that we are looking at a product. The base tells us to use 5 as the repeated factor and the exponent tells us to use three factors of 5, thusly

5³ • 5 • 5 • 5 = 125

The above has three forms of the expression: 1) the exponential form (left), 2) the expanded form (middle), and the 3) simplified form (right). The dots between the 5's in the expanded form mean multiply.

Exponents allow us to write a product where a number is repeated as a factor without having to write the number over and over again. Exponential form is a short hand way of writing a product that has a repeated factor.

R.4 Factoring Polynomials

Polynomial: An algebraic expression of one or more terms written in descending order by power of the variable. Each term has at least three parts: 1) a coefficient, 2) a variable with an exponent that may or may not be written (the power of the variable), and 3) either an positive or negative sign for each term after the lead term.

To factor: to write a number as the product of its factors.

A factor: one of the numbers that are multiplied to produce a product.

Algebraic expression: a collection of constants, variables, grouping symbols, and operation signs that represents exactly one value. DOES NOT contain a relationship symbol such as an equals sign or one of the inequality signs.

Coefficient: the number being multiplied times the variable in a term, usually a constant.

Variable: a written symbol that respresents a number whose value is not known. Using variables as place holderes for unknown numbers allows us to write expressions that describe a situation where the value of a part of the number may change. By using variables, we can represent the context of the part that changes.

Lead term: English and math are read from left to right; therefore, the leftmost term in a polynomial is referred to as the Òleading termÓ because is leads the rest of the terms in the expression. ItÕs the term we read first. Positive lead terms do not require a positive sign, but negative lead terms do require a negative sign.

Product: the result of multiplication. Every product has 1 as a factor.

R.6 Radicals and Rational Exponents

Vocabulary R.6 

1. Conjugate binomials: Two binomials whose product is the difference of two squares; i.e.: (x + 2)(x - 2). NOTE: the binomials have the same terms but the sign of the second term is the opposite.
2. Like Radicals: Two radicals that have the same index and same radicand.
3. Perfect factor: A number whose exponent is evenly divisable by the index.
4. Radical Equations: Equations that have a variable in the radicand.
5. Radical Expression: A number written as a radical or product of a Real Number and a radical. Has three parts: radical sign, radicand, and index. (index√radicand)
   
6. Rationalizing the denominator: Multiplying the numerator and denominator of a radical fraction by the number that will remove all radical signs from the denominator.
7. Roots: The base which raised to the power of the index is the radicand.
8. Square root: The base that squared (raised to the second power) is the radicand.
9. Cube root: The base that cubed (raised to the third power) is the radicand.
10. Nth root: The base that raised to the nth power is the radicand. 
    1. If bⁿ = a, then b is the nth root of a
       
11. Rational exponents, part 1: If n is an Integer > 1, then
    1. a^1/n = n√a
    2. If a is a negative Real Number and n is an even positive Integer, then this is not a real number.
12. Rational exponents, part 2: If m and n are positive Integers and n/m is in lowest terms, then a^n/m = m√aⁿ

Remember: n is the exponent, m is the index and a is the radicand.