In the last section we saw how we could build up a complex tone by adding together pure sine waves. We also saw that whereas we could find the fundamental frequency of a complex tone by examining the time waveform, we could not glean any information about what other frequencies were present and in what amounts. This information can be obtained by the Fourier transform, a mathematical operation first mentioned in the previous section, that decomposes a time signal to show what frequencies it contains. As I said before we will not concern ourselves with the mathematical details we will just accept that the operation can be performed.

If the lack of detail is dissatisfying you can think about how you might accomplish the same task without mathematics. After all the ability to do the sort of mathematical calculations required to Fourier transform large signals has only existed for the last 20 years or so. There are a couple of answers. First, we will see later in the semester that the ear performs this transformation from time to frequency in a simple mechanical way. Another second means that should be plausible is to have a tunable filter that allows only a single frequency to pass through. By feeding a complex tone into the filter, tuning the filter across the audible range, and recording the frequencies at which signal comes through you could find what frequencies were contained within the tone. Keep this model in mind as we examine the following examples of spectral decomposition of signals.

As a starting example I am going to decompose the complex waveform that we built up from 2 pure sine waves in the previous section. Remember that the frequencies of the two sine waves were 262 Hz and 524 Hz with amplitude ratios of 1 and 0.8 respectively. Here is the plot as we saw before:

 

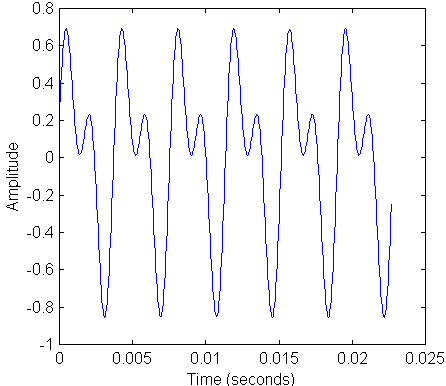
Now we Fourier transform this periodic waveform and obtain the following plot:

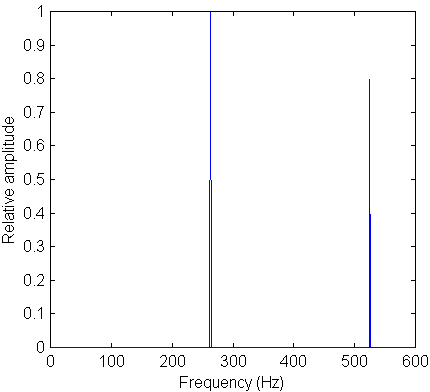
The horizontal axis is now frequency in Hertz. There are two sharp and extremely narrow peaks at 262 Hz and 524 Hz. The lower frequency peak rises to a height of 1 whereas the lower frequency rises to 0.8 on the vertical axis. We recognize these numbers as the relative amplitudes of the two sine waves that we added together to create our original complex tone.

You should be able to appreciate immediately the power of spectral analysis--we obtain information on what frequencies are contained within the signal and we know the amplitude of the higher harmonics relative to the fundamental. This information is much more than we could get from the time signal alone for which we couldonlycalculate the frequency of the fundamental.

As a next example let's examine a real recorded tone, namely the shaky harmonica tone that we looked at a couple of sections ago. Here is the time waveform again:

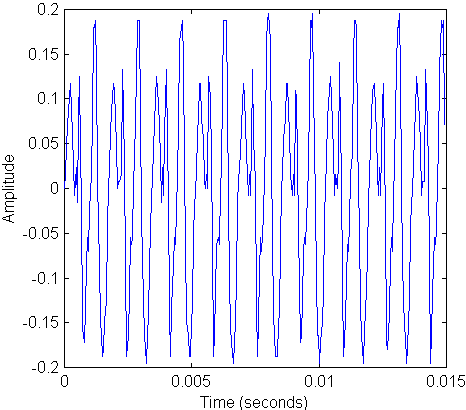
Remember we found that the period was 1.685 ms corresponding to a frequency of 593 Hz. Here is the Fourier transform of this waveform:

 

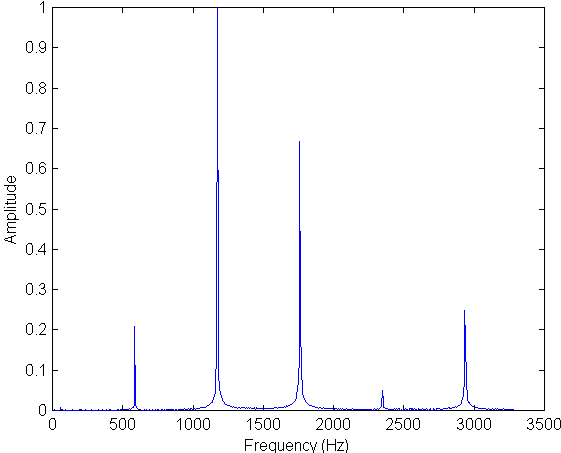
Sure enough there is a peak at 593 Hz that rises to about 0.2 on the relative amplitude scale. This peak is dwarfed by the second harmonic at a frequency of 2 x 593 = 1186 Hz and even by the third harmonic 3 x 593 = 1779 Hz! The fourth harmonic is negligible and the fifth harmonic is about the same size as the fundamental. Note that the peaks are not quite as sharp as for the first spectrum that I showed; there is a spread in the base of each peak. This results from the fact that in this second case I am examining a real signal (me playing the harmonica) rather than a digitally created signal formed by adding sine waves in the computer. The latter is pretty much perfect whereas when I play the harmonica note there are variations that make the signal slightly imperfect.

It is also sometimes surprising that we associate the pitch of this note with 593 Hz even though this frequency is relatively weakly represented in the signal. We will see in class that the pitch of the note would not changeeven if we completely removed the contribution at 593 Hz!

I mentioned earlier that there are (probably) no musical instruments that emit pure tones. All instruments have a characteristic mix of fundamental and higher harmonics--this mix is part (but only part!) of what allows us to distinguish a harmonica note from that of a trumpet or of a bassoon. The harmonic structure of the sound produced by an instrument is called thetimbreof the instrument. The timbre is not an absolute fixed quantity for an instrument, it can change depending on whether low notes or high notes are being played (for example the timbre of low and high notes on a piano may be quite different). The timbre can also vary depending onhowthe same note is played. Follow the link below to see an example of the difference in timbre of plucked guitar strings. This page also serves as the self test portion to this page. 

• Plucked Guitar String Example

<- Back