Pressure Amplitude: Quantitative Measurement of Sound

As we will discuss in this section decibels are a means of creating a logarithmic scale relative to some reference. Decibel scales are by no means confined to acoustics, there are decibel scales defined for use in electronics and optics. Even in acoustics there are a variety of different definitions of the decibel scale depending upon the quantity being used as a reference. Thus, to begin our discussion I want to cover the question of what parameters are measured in determining sound levels.

The most physically understandable quantity used in determining the size of a sound signal is the Pressure Amplitude. Pressure amplitude is a measure of the size of the variation in air pressure caused by a sound wave. In pure silence there is a constant pressure--atmospheric pressure. Atmospheric pressure is measured in newtons/meter2 and is approximately 105 N/m2. The atmospheric pressure varies a small amount over the space of hours or days--this is what they mean by high and low pressure centers on the weather map--however, we can consider it to be essentially constant on the time scale of sound waves.

A sound wave creates a variation in the normally constant air pressure that oscillates above and below the normal atmospheric level of 105 N/m2. The average size of the pressure variation away from the constant background level is the Pressure Amplitude of the sound wave. I am hiding a bit of complication in the word average; the pressure goes above (positive) and below (negative) the constant atmospheric background so a straight average would tend to give zero. The real average is a root mean square average which you might be familiar with if you have done some electronics. For a pure tone--a pure sine wave--the averaging process leads to a pressure amplitude that is reduced from the maximum amplitude by a factor of 0.707 (equivalent to dividing by the square root of 2). The relation between amplitude of the sine wave (measured from the background level to one extreme) to the pressure amplitude (average pressure excursion from the background) is shown in the figure below.

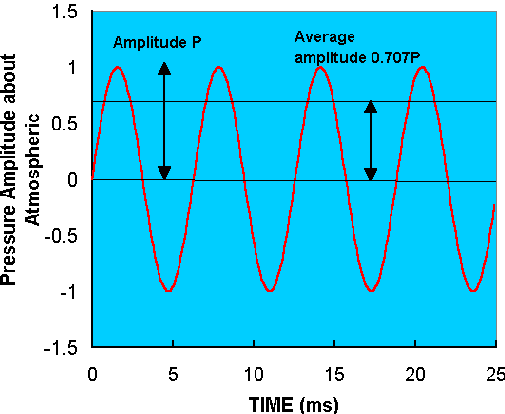
It is fairly simple to understand how a calibrated measurement of the pressure amplitude can be made using a microphone to convert the pressure variations into an electrical signal. By applying known pressure variations to the microphone the electrical signal can be calibrated to directly measure the air pressure variations. With suitable processing this pressure variation can be converted into the pressure amplitude. This function is performed by Sound Pressure Level (SPL) meters.

Our next concern is to address the question: how large is the pressure amplitude for typical sounds? To answer we begin by considering the pressure amplitude for the weakest sound that is audible to the average person. This value is referred to as the threshold of hearing (for obvious reasons). The pressure amplitude for the threshold of hearing is 2 x 10^-5 N/m². This is a standard value defined for a pure sine wave at a frequency of 1000 Hz. As we will see later in this class, our ability to hear is a strong function of frequency so the value is quite different at other frequencies. Of course the ability to hear also varies from person to person so this is an average for the human population.

It is instructive to compare the threshold of hearing value to the background air pressure. Remember the pressure amplitude is the average size of the pressure variation on the constant atmospheric background. By taking the ratio of the threshold of hearing pressure amplitude to atmospheric pressure we see that the weakest audible sound waves only create a variation in the background pressure of 0.00000003%. Pretty small. Now how about very loud sounds. The threshold of pain corresponds roughly to a pressure amplitude of 30 N/m² (a million times larger than the threshold of hearing). This value translates to pressure variations of 0.03% about the atmospheric background value. Even loud sounds do not vary the background air pressure by even 1%!

Sound Pressure Level: A Decibel Scale defined in Terms of Pressure Amplitude

Now that we understand pressure amplitude as one measure of the size of a sound signal lets look at the decibel scale defined for this quantity. The decibel scale for pressure amplitude is called Sound Pressure Level, typically abbreviated SPL, and designated in our text and in this course by the symbol L_p. The decibel SPL value for a sound with pressure amplitude P is given by the relation

L_P = 20log(P/P₀)

Note that there is one quantity in the equation that I have not defined yet namely P₀. Remember that I said at the beginning of this page that decibels are a relative measurement scale--in this case the sound pressure amplitude being measured P is determined relative to the value P₀. P₀ is an agreed upon value of 2 x 10^-5 N/m². You might recognize this value as the pressure amplitude for the threshold of hearing at 1000 Hz mentioned a couple of paragraphs above. This choice of reference values is of course intentional.

Lets look at two examples of how to move from a pressure amplitude to a SPL decibel reading and from a decibel value back to the pressure amplitude P.

Example 1

Find the decibel reading corresponding to a pressure amplitude P = 0.2 N/m².

Using the above definition for L_p we begin with the term in brackets on the right hand side of the equation by dividing P by P₀.

P/P₀ = 0.2/2x 10^-5 = 10000

Next we take the log of this value

log(10000) = 4

and multiply by 20 to get L_p

L_p=20 x 4 = 80 dB.

Note that we write dB standing for decibels after the final answer. Decibels are not actually a measurement unit because the decibel value depends on the agreed upon reference. Note that in the first step of the calculation we divide one pressure amplitude value by another eliminating all units!

Example 2

Find the pressure amplitude corresponding to a decibel reading of 35 dB.

In this case we know the left hand side of the equation ands as always we know the value of P₀=2 x 10^-5, thus we can write the equation

35dB = 20log(P / 2x10^-5)

To get P we first divide both sides by 20 to get

1.75 = log(P / 2x10^-5)

Now the step that often stumps folks whose algebra is rusty--we want to remove the log from the left hand side. From our review of logarithms we saw that the log of a number is the exponent that 10 would have to be raised to to get that number. Thus, 10 raised to the power 1.75 is P/2x10^-5! Think this step through to make sure it's clear. The result is that

10^1.75 = (P / 2x10^-5)

For the last step we race to our calculators, put in 1.75, hit the 10^x button, and then multiply by 2x10^-5 to get the final answer 1.12x10^-3 N/m². Note that our answer has the units of pressure N/m².

Self Test #1

Try the following questions that test your ability to work with the SPL decibel equation. These questions also illustrate some important properties of decibel scales so make sure you work and understand the problems.

1. Find the pressure amplitude that corresponds to the threshold of pain decibel reading of 120 dB.
2. Calculate the decibel reading for a pressure amplitude of P = 7 x 10^-3 N/m².
3. Calculate the decibel reading for a sound at the threshold of hearing, i.e. P = 2 x 10^-5 N/m².
4. Calculate the decibel reading for a sound with P = 1.5 x 10^-5 N/m². This sound pressure amplitude is below the threshold of hearing.
5. Calculate the pressure amplitudes for SPL readings of 26 dB and 20 dB. How are the two pressure amplitudes related?
6. Calculate the pressure amplitudes for SPL readings of 56 dB and 50 dB. Again how are the two pressure amplitudes related? Notice a pattern?

Intensity and its Relation to Pressure Amplitude

Although pressure amplitude is one measure of the presence of a sound wave it is not the only one, nor is it always the most convenient parameter to use. A second important quantity in characterizing sound waves is called Intensity. Intensity is a measure of the sound energy that passes through a given area each second. Now energy per second is measured in Watts (a 60 Watt light bulb gives out 60 Joules of energy each second) thus intensity has units of Watts/m². In class we should already have talked about (or we will cover soon) the fact that waves carry energy and how, from a point source, the energy is spread over an increasingly larger area as the wave spreads out. From this discussion we concluded that in the free field limit the intensity of a wave drops off as the inverse square of the distance from the source.

The point that I want to make here is that the intensity is related to the pressure amplitude. In particular the energy in a wave is proportional to the square of the pressure amplitude. In other words if I double the amplitude of the wave I quadruple the energy carried by that wave. You will see how this relation becomes important in the coming comparison of the decibel scale defined with intensity to the SPL scale we have already examined.

Sound Intensity Level

The decibel scale defined in terms of the sound wave intensity is given by the relation

L_l = 10log(l / l₀)

where I is the intensity of the sound wave and I₀ is the reference value. The form of the equation looks similar to that for SPL that we defined above except that the multiplier in front of the log is 10 instead of 20. The reference value I₀ is the threshold of hearing intensity at 1000 Hz and is 10^-12 W/m². The intensity decibel scale is called the Sound Intensity Level abbreviated SIL and, in common with our text, the corresponding symbol is L_I.

Because the SPL and SIL scales are both referenced to the threshold of hearing value the decibel reading for the two scales can usually be assumed to be identical in most simple situations. In practice there are some subtleties because the pressure amplitude at a point is the result of waves coming from all directions whereas the intensity implies that we have to define a surface and a direction through which the energy flows. We will not concern ourselves with these points but it's good to be aware that they exist.

We can understand the origin of the factor of 2 difference in the multipliers for the definitions of SPL and SIL using the square relation between pressure amplitude and intensity and our rules for logarithms. Lets begin with the SPL definition but lets write 20 = 10 x 2.

L_P = 10x2log(P / P₀) = 10log(P / P₀)² = 10log(l / l₀)

In the second step we took the 2 inside the logarithm and used it to raise the pressure amplitude ratio to the power 2. Look at Rule of Logarithm number 2. Finally, because the intensity is related to the square of the pressure amplitude we replace the pressure amplitude ratio squared with the intensity ratio.

We will see in the next unit why it is sometimes easier to work with intensity rather than pressure amplitude; however, the mathematics of manipulating the two equations is very similar because of the parallel forms of the equations. Test yourself with these quick self test questions.

Self Test #2

1. What is the intensity of a 90 dB sound?
2. What is the intensity of a -3 dB sound?
3. What is the intensity of a 0 dB sound?
4. What is the SIL of a sound with intensity of 5 x 10^-6 W/m²?
5. What is the SIL of a sound with 0.5 W/m²?

Love the hat! Who's your friend?

 

<- Last Next ->