Combining Decibel Quantities

We have defined the SPL and SIL decibel scales, now I want to examine the mathematics of combining decibel readings.  In particular we will see that it is not possible to merely add decibel quantities and get anything sensible.  For example, if I have two uncorrelated (we'll define this) sources each creating sounds of 30 dB then when played together they emit 33 dB! What kind of crazy math is that you say? Well it all goes back to the fact that we are dealing with a multiplicative rather than additive scale when we use logarithmic quantities such as decibels. The central notion of this section is that to combine two or more decibel readings requires converting each value back to the corresponding intensity or pressure amplitude, adding these values appropriately, and finally converting the sum back into a decibel quantity.  The tricky part comes from the fact that there is a different procedure for combining intensity and pressure amplitude values. Read on.

Combing SIL Readings

We will start with the procedure for combining intensity values because it is the most straightforward.  To combine two SIL readings requires that I follow the following simple prescription: (1) Convert the two SIL values into the corresponding intensities I1 and I2, (2) Add the two intensities I1 + I2 = Itotal, (3) convert Itotal back into a decibel reading.

This procedure assumes that the two sources of sound that give rise to the SIL values are uncorrelated.  We will define correlated and uncorrelated sources a bit more carefully below, however, for now you can take uncorrelated to mean that the sources create sound independently of each other e.g. two radios tuned to different stations. Let's look at an example and then you can try a few self test questions.

Example 1

Two electric guitars create SIL values of 45 dB and 50 dB respectively.  What dB reading would you expect when both are played simultaneously. 

Following the above procedure: 

1. 45 dB corresponds to an intensity I1 = 3.16 x 10-8 W/m2, 50 dB corresponds to an intensity of I2 = 1 x 10-7 W/m2.  If you can't figure out how I got these values you need to review the previous web page! 

2. Add the two intensity values to get the total intensity Itotal =  I1 + I2 = (3.16 + 10) x 10-8 = 13.16 x 10-8 W/m2. 

3. Convert the total intensity back into a dB reading. You should be good at this by now.  The answer is 51.2 dB. 

Combining the SIL values by adding the corresponding intensities is fairly simple.  Try these self test exercises. 

Self Test 1 

1. Find the combined dB reading for two uncorrelated sources each with with SIL of 100 dB.
2. Find the combined dB reading for two uncorrelated sources with SIL values of 0 dB and 3 dB.
3. Find the combined dB reading for two uncorrelated sources with SIL values of 0 dB and -3 dB.
4. Find the combined dB reading for 10 sources each with SIL of 40 dB.

Combining SPL Readings

The process of combining SPL values is a little more complex.  I will outline the process in step-wise fashion as I did for the SIL section.  As you will see the step of combining pressure amplitudes is not as simple as the addition we used for the intensities.  I will discuss why there is this difference and on the way we will learn more about the concept of correlated and uncorrelated sources. 

First the procedure for combining SPL values: (1) Convert the two SPL values into the corresponding pressure amplitudes P1 and P2, (2) Combine the two pressure amplitudes according to  P12 + P22 = P2total, (3) convert Ptotal back into a decibel reading.

The only tricky part is step (2) in which we add the squares of the pressure amplitude values to obtain the square of the total pressure amplitude.  Don't forget to take the square root of the total pressure amplitude obtained in step (2) before using it in step (3).   You should be asking yourself why do we need this procedure to combine the pressure amplitudes?  One mathematical way of looking at the process is to reason that because the intensity is proportional to the square of the pressure amplitude and because we add intensities we must therefore add the squares of the pressure amplitudes.  Okay, that's one line of reasoning but it does not give an understanding of the physical reason underlying this combination process.  I want to look at the subject a little more closely. 

To understand the physical reason for the averaging process we must examine the process of combining wave amplitudes.  In the examples below I assume that we are combining two equal amplitude pure sine waves of the same frequency.  Of course the waveforms associated with real sounds consist of many frequencies and amplitudes; however, as we will see later in the semester, these complex waveforms can always be decomposed into a sum of individual pure sines. 

Lets begin by assuming that we have correlated sound sources.  By correlated we mean that each source creates exactly the same wave amplitude at the same time at a given point.  How would we make a correlated source in practice?  Well if we took a one electrical signal, split it, and fed it to two identical speakers AND we stood equidistant from each speaker we would have correlated sounds.  By splitting one signal we ensure that each speaker is creating high and low pressure wave amplitudes at the same time. The reason that we stand equidistant from the speakers is to ensure that the sound waves that reach us have traveled the same distance and thus arrive in phase.  A pictorial representation of such in-phase waves is given in the figure below.

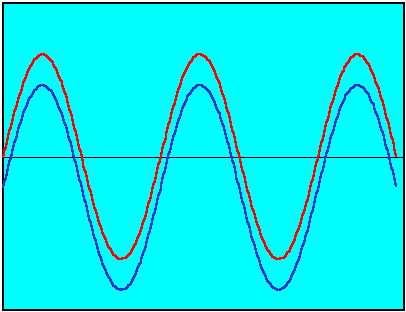
The blue curve has been offset by a small amount because otherwise the two curves would overlap precisely. Unless you are racing ahead of the pack, we should by now have talked in class about the Superposition of Waves which states that when two waves occupy the same point in space the total wave amplitude at that point is just the sum of the amplitudes of the individual waves.  Thus, for correlated waves the pressure amplitudes add, i.e. P1 + P2 = Ptotal!  This result goes against what we covered previously for combining pressure amplitudes using the squared values; however, we were also careful to say above that our combination rules for decibel quantities only worked for uncorrelated signals and the direct addition is only valid in this particular case of correlated signals.

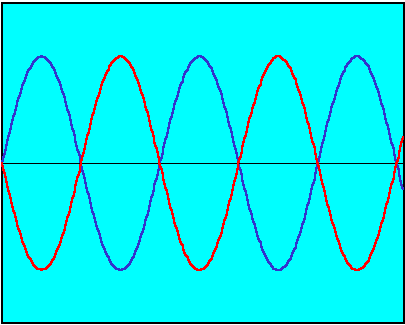
So let's consider the case of uncorrelated signals.  There is now no guarantee that two sound waves will arrive at the same point in phase.  Sometimes they will be, but they are just as likely to be in complete anti-phase (180 degrees out of phase) as shown in this figure,

or any value in between as in this figure. 

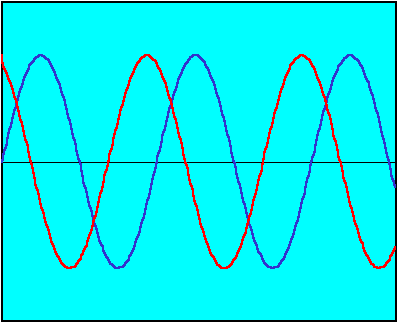
As time goes by the net result will be some average value between the extreme cases of completely in-phase and out-of-phase. 

Does the sum of the squares method of adding the pressure amplitudes make sense?  The complete mathematical treatment is a little too involved for our purposes but lets look at whether the result is within the correct range.  Imagine we are combining two sound waves each with pressure amplitude 1.  If they are in phase then at the peak the maximum amplitude is 1 + 1 = 2.  Similarly if they are in complete antiphase as in the second graph above the sum of the amplitudes is 1 - 1 = 0.  Our average value should lie somewhere in the range of 0 to 2.  Well the square and add method give P2total = 12 + 12 = 2. Or in other words Ptotal is 1.414 (the square root of 2) which does lie between 0 and 2 as we expected. 

I know this last material can be a bit bewildering the first time through.  However, I want to give you an accurate sense of the complications that occur when one is combining quantities associated with waves. To test your understanding of the SPL combination formula try the following self test.

Self Test 2 

1. Two uncorrelated sources have SPLs of 30 dB and 32 dB.  What is the combined SPL?
2. Two uncorrelated sources have SPLs of 100 dB each.  What is the combined SPL of both played together?
3. Now consider the same problem but with 2 correlated sources of 100 dB.  What change do you make in the calculation?
4. What is the SPL of 1 million uncorrelated sources each with SPL of 0 dB?

Here endth the last section on Logarithms and decibel scales.

<- Last